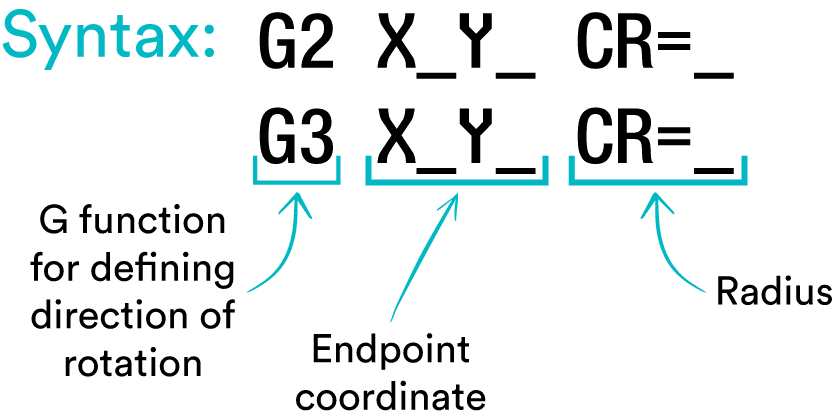
CR Circular interpolation with radius
CR - Circular interpolation with radius, tips for use and analysis of some details related to it
INSIGHT
In today’s lesson we covered the second circular interpolation in order of its most use: circular interpolation with radius. In first place as already mentioned we have circular interpolation with circle center, which always guarantees double verification of the input data.
In this focus we will look at some details related to circular interpolation with radius by taking up the syntax first.
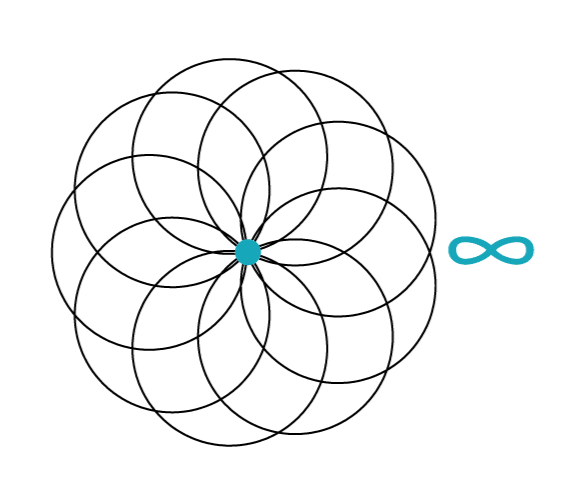
The first aspect I would like to focus on is the use of circular interpolation to perform entire circumferences. Due to a properly mathematical issue, it is not possible to perform complete circumferences (equal to 360°) by programming them in a single block using circular interpolation with radius.
The reason is simple: if I programmed a full circumference it would mean that the end point would correspond to the starting point. In doing so, the numerical control would find itself having to choose among infinite circumferences all with the same radius. In fact, for integer circumferences it is essential to define the center of the circle. We could get around this problem by programming two half-circles.
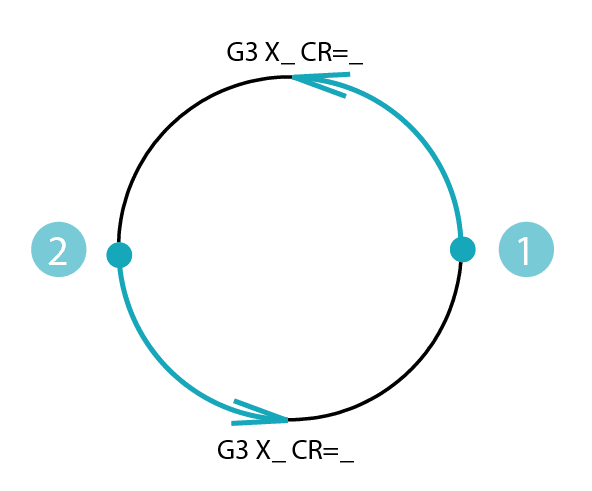
In the case of semicirconferences the value of the radius we could express either positive or negative since they are 180° arcs. In any case I have reported this solution for didactic reasons but the advice is always to use circular interpolation with circle center for programming integer circumferences.
EXERCISE
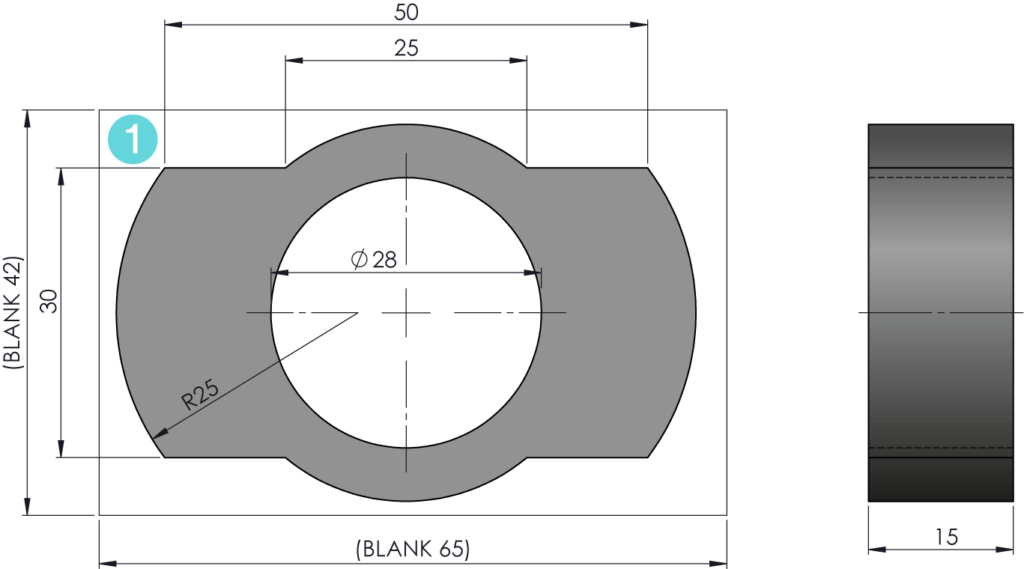
In the lesson attachment you will find the file SIE03_LEZ04_EXERCISE2. This is an exercise along the lines of what was done in the class. You will have to do the contour using a d16 milling cutter using circular interpolation with circle center and circular interpolation with radius appropriately.
The blank dimensions are given in round brackets and are 65 × 42. It is recommended to approach the contour at point n° 1 using a G147 tangent linear approach and a G247 tangent circular detachment.
Good job!

